Ethics
We received approval to access and analyze deidentified genetic and phenotypic data from the two cohorts from SFARI Base and the Princeton University IRB Committee in the Office of Research Integrity. Our research complies with all relevant ethical regulations.
Participants
We restricted our sample to children aged 4 to 18 years from the SPARK cohort33, including both autistic individuals and their nonautistic siblings. The SPARK Phenotype Dataset V9 battery assays core autistic traits (social, language-related and repetitive behaviors), cognitive measures and co-occurring behavioral features (anxiety, aggression and so on). Measures in SPARK with a sufficiently high overlap among participants were selected to maximize the cohort size while maintaining breadth of phenotype data. These measures included the background history (a form that asks parents to report on ages at developmental milestones), SCQ34, RBS-R35 and CBCL36 (Supplementary Note). All autistic children with data from these four phenotype measurement tools were included in the mixture modeling analysis. The same sample of individuals was measured repeatedly. To maximize our sample and feature sizes, we excluded features with less than 90% completeness across the cohort and only included individuals with complete measures across the remaining features. Our resulting cohort included 239 item-level and composite phenotype features and 5,392 individuals in SPARK alone. The cohort had a mean age of 8.56 years with a standard deviation of 3.15 years. Our sibling cohort comprised 1,972 paired siblings (related to at least one proband in the autistic cohort) with no ASD diagnosis, age less than 18 years and available whole-exome sequence data. Of the four phenotypic measures, only the background history and SCQ were available for SPARK siblings. For trio-based analyses, we only used complete trios in SPARK (n = 1,992 probands, n = 837 paired siblings). In both our phenotypic and genetic analyses, only individuals who passed quality control and had complete data were included.
Mixture modeling analyses
Mixture model and covariates
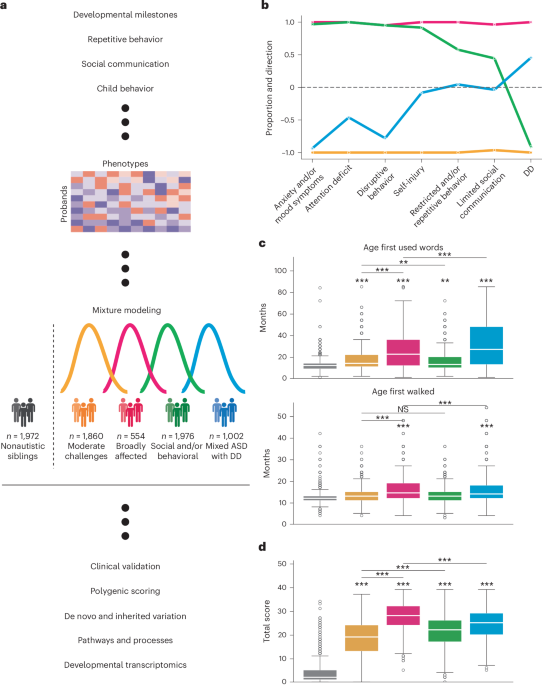
The phenotype matrix included 5,392 individuals and 241 features (239 training features, two covariates). We used the StepMix package (v.1.2.5)49 to fit a model and predict labels for each individual using a GFMM approach. This model expands the Gaussian mixture model by using different probability density functions (Gaussian, binomial or multinomial) to model continuous, binary and categorical features. We trained a one-step model with covariates (sex and age at evaluation) and hyperparameters n_init = 200, n_components = 4. The model computed four probabilities per individual to assign each individual to a latent class.
Stability and robustness analyses
To demonstrate robustness and stability, we trained 2,000 models with random initializations. We ranked models by their log likelihoods and retained the top 100 models for further analysis. To demonstrate robustness to perturbations of the sample set, we trained 100 independent models (each with 20 random initializations) with a subsampling rate of 50% of the individuals in the sample. In each analysis, we computed the proportion of individuals assigned to the same class, as well as the feature concordance across categories of phenotypes.
Exploratory class enumeration
The main tunable hyperparameter of the GFMM is the number of latent classes. It is recommended that this number is chosen by identifying an ‘elbow’ in statistical measures of model fit, in combination with careful consideration of practical interpretability50,51,52. We tuned this hyperparameter in a multistep process that considered various statistical measures of model fit and indicators of optimality. We evaluated models with 1–12 components and computed the validation log likelihood, Akaike information criterion, consistent Akaike information criterion, BIC, sample-size-adjusted BIC, likelihood ratio test statistics (Lo–Mendell–Rubin likelihood ratio test) and more, over 50–200 independent runs with randomly generated seeds (Supplementary Note).
Interpretation
We consulted clinical collaborators on the interpretability of multiple candidate models and found that the four-class solution offered the best phenotypic separation and most clinically relevant classes. Less complex models offered insufficient phenotypic reduction, whereas more complex models overfitted our data, resulting in fragmented classes that were challenging to interpret owing to mixed enrichments within feature categories. Phenotypic descriptions for three-, five- and six-class model solutions can be found in Extended Data Fig. 2. The final four-class breakdown was as follows: Moderate challenges, n = 1,860 (34%); Broadly affected, n = 554 (10%); Social/behavioral, n = 1,976 (37%); Mixed ASD with DD, n = 1,002 (19%). Sex breakdown and percentages by class were as follows: Moderate challenges, 1,459 males (78%), 401 females (22%); Broadly affected, 441 males (80%), 113 females (20%); Social/behavioral, 1,475 males (75%), 501 females (25%); Mixed ASD with DD, 799 males (80%), 203 females (20%).
As outlined above, there was not one clear indicator for this parameter choice. We evaluated a rigorous combination of statistical measures, combined with interpretability, to select our final model: a four-component model that provided the best balance of model fit, complexity and interpretation.
Phenotype categories
To phenotypically define and interpret our model outputs, we grouped the 239 features used in training the GFMM into seven factors previously defined in the literature35,37,38,39. Our categories included: limited social communication, restricted and/or repetitive behavior, attention deficit, disruptive behavior, anxiety and/or mood symptoms, developmental delay and self-injury. Each category was a composite of features assigned based on prior grouping evidence.
To more thoroughly examine how the factors defined the four phenotype classes, we performed the following analysis: first, we computed the enrichment (upper-tail significance) or depletion (lower-tail significance) of each feature in each class relative to the other three classes. For binary variables, a one-sided binomial test was used. For categorical and continuous variables, a one-sided independent t-test was used. Benjamini–Hochberg multiple hypothesis correction was performed for each autism class and direction of enrichment. We then computed the proportion of features with upper-tail and lower-tail significance in each category and class. At this stage, features were excluded based on three criteria: (1) features that had no significant enrichment or depletion in any class; (2) continuous or categorical features with Cohen’s d values between −0.2 and 0.2 across all classes; and (3) binary features with FE of less than 1.5 across all classes. This resulted in 220 contributory features. After computing the proportion of features enriched or depleted in each class and category, we negated the depleted proportions and summed them with the positive enriched proportions. This enabled us to compute a total proportion and direction of significant features for each category and class. This score represented the ‘affinity’ of the class towards a phenotype category relative to other probands.
Phenotypic replication in the SSC
We replicated the four SPARK phenotype classes in an independent cohort, the SSC40. We first extracted, processed and integrated the same phenotype measures from SSC that were used in the SPARK model: SCQ, RBS-R, CBCL 6–18 (only composite scores) and a form consisting of parent-reported timing of developmental milestone attainment. We identified 108 phenotype features that were present in both SPARK and SSC. To demonstrate the generalizability of the SPARK model to SSC, we trained a model on only the SPARK data for the 108 common features with the same hyperparameters as the model described above (n = 6,393 individuals in SPARK with complete data for the 108 features). We compiled the same features for n = 861 individuals in SSC who had complete data across the training features. We then applied the trained model to the SSC test data and predicted a class label for each individual from SSC. At this point, we excluded noncontributory features post hoc based on only the training data and according to the criteria described above. We obtained the proportion and direction of enrichment for each class and category across both SPARK and SSC. The Pearson’s correlation coefficients between SPARK and SSC for each of the seven phenotype categories were 0.98, 0.92, 0.94, 0.92, 0.89, 0.97 and 0.98.
Next, we obtained a significance of overall model similarity with two permutation tests. First, we randomly shuffled the class labels of SSC participants for n = 10,000 repetitions, obtaining a distribution of chance correlations between SPARK and SSC. We then compared the true correlation between SPARK and SSC (unshuffled labels) to the chance correlation distribution, allowing us to obtain a P value for overall model similarity that accounted for chance correlations. Second, we shuffled the SPARK sample data 1,000 times, each time training an independent model on the shuffled phenotypes, and projected those permuted clusters onto the SSC to test the concordance of the permuted cluster projection. We then compared the distribution of correlations with permuted cluster projections to the correlation with the real cluster projection.
External phenotypic validation
Phenotype measures that were available for the majority of our cohort but were not included in model training were used for external validation of the classes and exploratory phenotypic associations of clinical and diagnostic variables. The majority of individuals in our sample cohort (n = 5,381) had a complete or nearly complete basic medical screening form and self-reported (or parent-reported) registration form available. We computed the FE and P values (one-sided binomial test) for each basic medical screening diagnosis within each class compared to nonautistic siblings. For the registration form, we tested for enrichment using one-sided independent t-tests for continuous and categorical variables and one-sided binomial tests for binary variables. We also tested all class–class comparisons for every feature. We performed Benjamini–Hochberg correction to correct for multiple comparisons.
Genetic analyses
Polygenic scores
The most recent well-powered GWAS for ASD and several ASD-related traits and co-occurring conditions were used to compute PGS for the subset of our cohort with genotyping array data and European ancestry (determined by a self-reported race of white) passing some basic quality-control metrics (n = 2,294 autistic individuals, n = 426 nonautistic siblings). Genotypes were determined from Infinium Global Screen Array BeadChips available from SPARK33. Summary statistics were downloaded and uniformly processed before computing PRS with PLINK’s clumping algorithm53. Results were regressed by sex and the first six principal components to control for ancestry. All GWAS statistics used were based on populations of European ancestry. Adjustment for multiple comparisons was performed for each GWAS using Benjamini–Hochberg correction.
DNV calling and filtering
DNVs were called using the HAT41 software for all complete trios in our proband and sibling cohort with whole-exome sequence v.3 data (n = 2,013 probands, n = 1,013 paired siblings) from the variant call format files released by the SPARK Consortium. Briefly, this pipeline, which was optimized for whole-genome sequencing and whole-exome sequencing data, used variant calls from both DeepVariant (v.1.1.0)54 and GATK HaplotypeCaller (v.4.1.2.0)55 to identify variants that appeared in both variant call sets in the child (genotype of 0/1 or 1/1) but not in either parent (both genotypes 0/0). Variants were then filtered based on several quality metrics including read depth, genotype quality score and genomic regions. Variants in recent repeats, low complexity regions and centromeres were filtered out. We used the default values for the filtering parameters of minimum depth = 10 and minimum genotype quality score = 20. For filtering and quality control of DNVs, individuals with a high variant count (>3 s.d. above the mean across all trios) were excluded from the analysis, and nonsingleton DNVs (variants appearing in multiple SPARK families) were removed from further processing and analysis. This pipeline identified an average of 2.72 DNVs per proband (s.d. = 2.20) and 2.67 DNVs per sibling (s.d. = 1.63).
Rare inherited variation
The DNV pipeline was adapted to identify inherited variants using the same quality metrics. Inherited variants were identified as variants appearing in a child (genotype of 0/1 or 1/1) and in at least one parent (either genotype 0/1 or 1/1). They were then filtered in the same way as the DNVs to identify a high-confidence set of inherited variants. We identified an average of 41,725.2 inherited variants per proband (s.d. = 2,580.7) and 41,778.9 inherited variants per sibling (s.d. = 2,314.6). In all analyses, rare inherited variants were defined as inherited variants with an allele frequency
Gene sets and resources
We computed variant enrichments in seven different gene sets, including the set of all protein-coding genes from GENCODE v.29 (Supplementary Data). The SFARI gene set was extracted from SFARIGene and included category 1 genes only19,22. The Satterstrom gene set was retrieved from ref. 9. The rest of the gene sets were retrieved from ref. 44 and included genes with pLI > 0.9 from ExAC56, predicted ASD risk genes (FDR 6 and target genes of FMRP45. Finally, brain-expressed genes were selected using the expression table from GTEx v.7 (gene median transcripts per million per tissue)46. The genes selected were those whose expression in brain tissue was at least five times higher than the median expression across all tissues. The high-constraint and moderate-constraint gene sets were selected using pLI scores from gnomAD42.
Count-based burden analyses
For analyses of de novo and inherited variation, we analyzed the distributions of variant count burden for each class of probands or siblings. After extracting de novo and inherited variants for each individual, we ran the variants through Ensembl’s Variant Effect Prediction57 tool (release 111.0) with the –pick flag (most severe consequence) and the LOFTEE42 (v.1.0.4) and AlphaMissense58 plugins. To predict LoF variants, we flagged variants with the following predicted consequences: stop gained, frameshift variant, splice acceptor variant, splice donor variant, start lost, stop lost and transcript ablation. We further subset the variants to only include those flagged as high-confidence (‘HC’) by LOFTEE. To predict high-confidence missense mutations, we flagged variants with the following predicted consequences: missense variant, inframe deletion, inframe insertion and protein-altering variant. We further subset the variants to those predicted as ‘likely pathogenic’ by AlphaMissense. Some individuals had zero exome-wide calls for DNVs (n = 91 probands and n = 67 siblings). We accounted for their variant counts in each count-based analysis of DNVs.
We aggregated the counts of dnLoF, dnMis, rare inherited LoF variants and rare inherited missense variants for each individual. Modeling the variant counts as a distribution for each class and siblings, we performed hypothesis testing (one-tailed independent t-tests) followed by Benjamini–Hochberg correction for each variant class. Hypothesis testing was performed for all class–sibling and class–class comparisons.
Gene set and OR analyses
We computed the gene-set-specific variant burden counts and repeated the same hypothesis testing procedure using one-sided independent t-tests followed by Benjamini–Hochberg correction. All proband variant count distributions were tested against the sibling variant count distribution, and each class was also tested relative to all out-of-class probands and other classes. ORs were computed for each phenotype class and gene set. All comparisons were made for each class against siblings using Fisher’s exact tests followed by Benjamini–Hochberg correction for each gene set and variant type separately.
GO term analysis
To extract the top disrupted biological processes for each class, we flagged dnLoF and dnMis variants present in all protein-coding genes across individuals in each class. To extract the top GO biological processes and molecular functions for each class, we used ShinyGO 0.80 (ref. 59) (results generated on September 27, 2024), which computes FE and FDR enrichment values using a hypergeometric test, with all protein-coding genes as background. We selected the terms by FDR enrichment and sorted for top terms by FE values. For the Moderate challenges, Social/behavioral and Mixed ASD with DD classes, we used an FDR cutoff of 0.05. For the Broadly affected class, we used an FDR cutoff of 0.1 owing to the smaller class size.
Developmental gene expression analysis
We leveraged a single-cell human prefrontal cortex dataset collected from postmortem tissues at six different stages of development48. We used Table S3 from ref. 48 to retrieve brain development gene sets (termed devDEGs) for prefrontal cortex cell types that followed one of four general gene trend patterns defined by the authors: ‘up’ (increasing expression throughout stages, with the highest expression in late stages), ‘trans up’ (increasing expression in earlier stages, peak in middle stages, followed by a decline in later stages), ‘down’ (declining expression throughout stages, with the highest expression in the fetal stage) and ‘trans down’ (declining expression in early stages, lowest expression in middle stages and increasing expression in late stages). devDEGs were identified through a differential expression analysis of the six developmental stages (fetal, neonatal, infancy, childhood, adolescence, adulthood). Although 14 major trajectories were identified, we opted to use the four general gene trends for clarity and interpretability. We further combined clusters of cells into the four identified major cell type categories: principal excitatory neurons, inhibitory interneurons (medial ganglionic eminence), inhibitory interneurons (caudal ganglionic eminence) and glia. This was done by taking the union of devDEGs associated with each major cell-type category. We conducted a count burden analysis of dnLoF mutations in each phenotype class compared to nonautistic siblings and for every class–class comparison and computed FE values (of the means) and P values (one-sided independent t-tests) followed by Benjamini–Hochberg correction.
To compare the constraint of genes affected in the Moderate challenges and Mixed ASD with DD classes, we extracted the genes with high-confidence dnLoF variants in each class for the following combinations of gene expression trends and cell types: down in principal excitatory neurons, down in inhibitory interneurons (medial ganglionic eminence), down in inhibitory interneurons (caudal ganglionic eminence) and down in glia. These categories displayed enrichment for dnLoF variants across both classes. We extracted the pLI values for affected genes in each class and conducted a one-tailed Mood’s median test to determine whether the distributions of pLI scores were significantly different between the two classes.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.